clear all;
fs = 44100;
N = 5; type=3;
L = floor(N/2);
G1 = 0; G2 = 18.0618;
if type==0,
gB = 3;
else
gB = 0.01;
end
G0 = 0; gs = 0.01;
N1 = 1000; N2 = 2000; N3 = 3000;
f0 = 400;
Df1 = 20; Df2 = 100;
fsig = 400; wsig = 2*pi*fsig/fs;
for n=1:N3+1,
if n<=N1+1,
Df(n) = Df1;
G(n) = G1;
elseif n<=N2+1,
Df(n) = Df1 + (Df2-Df1)/(N2-N1) * (n-N1-1);
G(n) = G1 + (G2-G1)/(N2-N1) * (n-N1-1);
else
Df(n) = Df2;
G(n) = G2;
end
if G(n)<gB,
GB(n) = G(n)/2;
else
GB(n) = G(n)-gB;
if type==2, GB(n) = gB; end
end
if GB(n)<gs,
Gs(n) = GB(n)/2;
else
Gs(n) = gs;
end
end
w0 = 2*pi*f0/fs; Dw = 2*pi*Df/fs; c0 = cos(w0); s0 = sqrt(1-c0.^2);
U = zeros(L+1,4);
V = zeros(L+1,4);
W = zeros(L+1,4);
S = zeros(2,2,L+1);
Z = zeros(L+1,8);
for n=1:N3+1,
x(n) = sin(wsig*(n-1));
switch type
case {0,1,2}
[Beq,Aeq,Bhat,Ahat] = hpeq(N, G0, G(n), GB(n), w0, Dw(n), type);
case 3
[Beq,Aeq,Bhat,Ahat] = hpeq(N, G0, G(n), GB(n), w0, Dw(n), 3, Gs(n));
end
[ycn(n),U] = df2filt(Bhat,Ahat,w0,x(n),U);
[ytr(n),V] = transpfilt(Bhat,Ahat,w0,x(n),V);
[gamma,d] = dir2latt(Bhat,Ahat);
[ynl(n),W] = nlattfilt(gamma,d,w0,x(n),W);
[A,B,C,D] = dir2state(Bhat,Ahat);
[yst(n),S] = statefilt(A,B,C,D,w0,x(n),S);
[gamma,dec] = dir2decoup(Bhat,Ahat);
[yde(n),Z] = decoupfilt(gamma,dec,w0,x(n),Z);
end
t = (0:N3); Gt = 10.^(G/20);
set(0,'DefaultAxesFontSize',18);
figure;
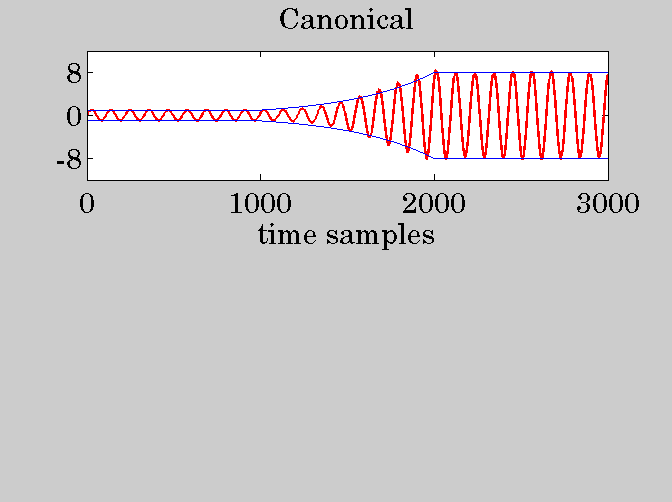
subplot(2,1,1);
plot(t,ycn,'-r');
hold on;
plot(t,Gt,'-b','LineWidth',0.5);
plot(t,-Gt,'-b','LineWidth',0.5);
hold off;
ylim([-12,12]); xlim([0,N3]);
ytick([-8,0,8]); xtick(0:1000:N3);
title('Canonical');
xlabel('time samples');
print -deps fig16c1.eps
figure;
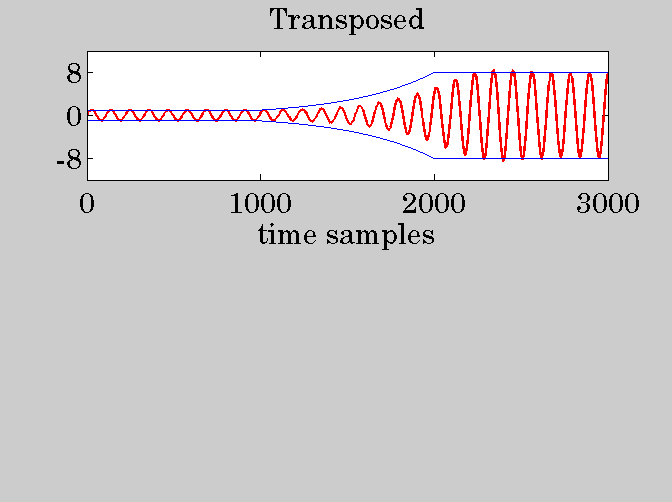
subplot(2,1,1);
plot(t,ytr,'-r');
hold on;
plot(t,Gt,'-b','LineWidth',0.5);
plot(t,-Gt,'-b','LineWidth',0.5);
hold off;
ylim([-12,12]); xlim([0,N3]);
ytick([-8,0,8]); xtick(0:1000:N3);
title('Transposed');
xlabel('time samples');
print -deps fig16c2.eps
figure;
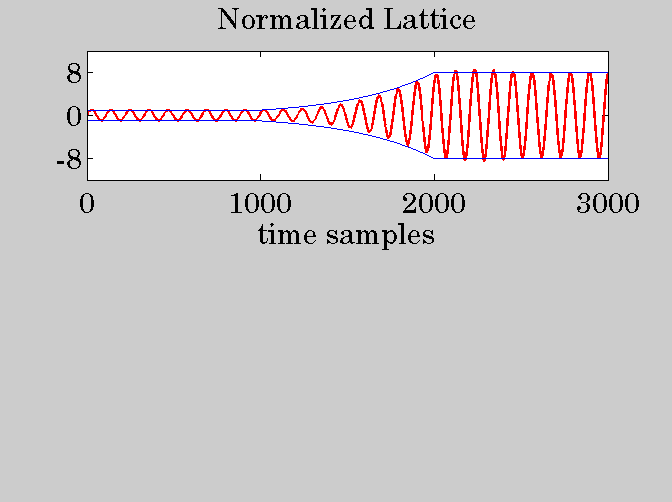
subplot(2,1,1);
plot(t,ynl,'-r');
hold on;
plot(t,Gt,'-b','LineWidth',0.5);
plot(t,-Gt,'-b','LineWidth',0.5);
hold off;
ylim([-12,12]); xlim([0,N3]);
ytick([-8,0,8]); xtick(0:1000:N3);
title('Normalized Lattice');
xlabel('time samples');
print -deps fig16c3.eps
figure;
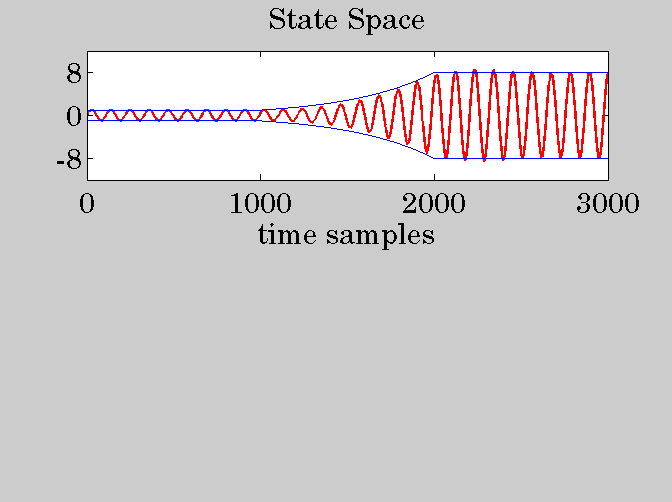
subplot(2,1,1);
plot(t,yst,'-r');
hold on;
plot(t,Gt,'-b','LineWidth',0.5);
plot(t,-Gt,'-b','LineWidth',0.5);
hold off;
ylim([-12,12]); xlim([0,N3]);
ytick([-8,0,8]); xtick(0:1000:N3);
title('State Space');
xlabel('time samples');
print -deps fig16c4.eps
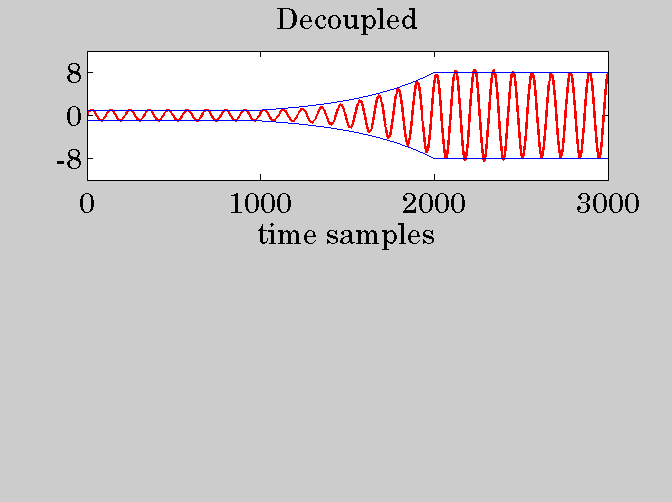
figure;
subplot(2,1,1);
plot(t,yde,'-r');
hold on;
plot(t,Gt,'-b','LineWidth',0.5);
plot(t,-Gt,'-b','LineWidth',0.5);
hold off;
ylim([-12,12]); xlim([0,N3]);
ytick([-8,0,8]); xtick(0:1000:N3);
title('Decoupled');
xlabel('time samples');
print -deps fig16c5.eps