clear all;
fs = 40; f0 = 4; Dfb = 2; w0 = 2*pi*f0/fs; Dwb = 2*pi*Dfb/fs;
[wb1,wb2] = bandedge(w0,Dwb); fb1 = wb1*fs/2/pi; fb2 = wb2*fs/2/pi;
f = linspace(0,20,501); w = 2*pi*f/fs;
N = 4;
type = 0;
G0 = 0; Gb=3; G = 12; GB = 9;
[B,A] = hpeq(N, G0, G, GB, w0, Dwb, type);
H = 20*log10(abs(fresp(B,A,w)));
figure;
plot(f,H,'b-');
hold on;
ylim([-8 14]); ytick(-6:3:12);
xlim([0,20]); xtick(0:2:20);
grid;
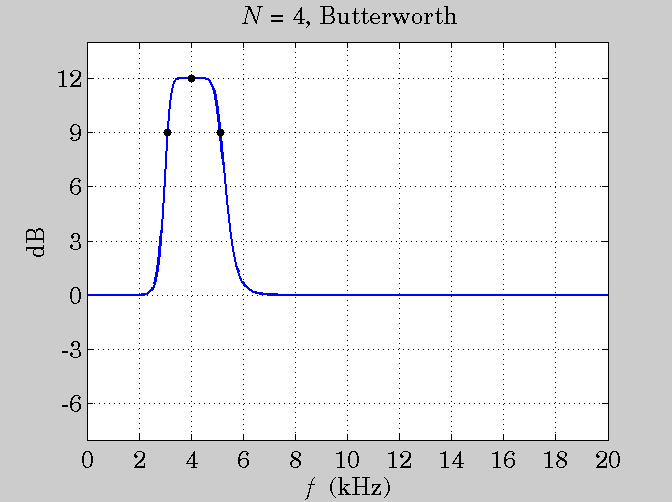
plot([fb1,f0,fb2], [GB,G,GB], 'k.', 'markersize',18);
hold off;
xlabel('{\it f} (kHz)');
ylabel('dB');
title('{\it N} = 4, Butterworth');
type = 1;
G0 = 0; G = 12; GB = 11.99; Gb = 9;
Dw = hpeqbw(N, G0, G, GB, Gb, Dwb, type);
[w1,w2] = bandedge(w0,Dw); f1 = w1*fs/2/pi; f2 = w2*fs/2/pi;
[B,A] = hpeq(N, G0, G, GB, w0, Dw, type);
H = 20*log10(abs(fresp(B,A,w)));
figure;
plot(f,H,'b-');
hold on;
ylim([-8 14]); ytick(-6:3:12);
xlim([0,20]); xtick(0:2:20);
grid;
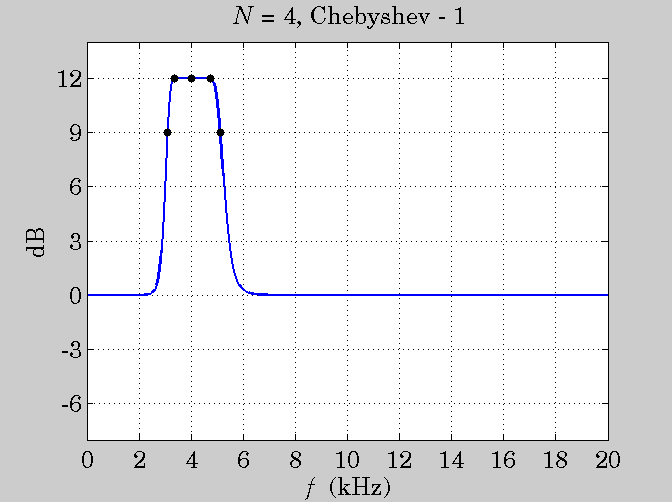
plot([fb1,f1,f0,f2,fb2], [Gb,GB,G,GB,Gb], 'k.', 'markersize',18);
hold off;
xlabel('{\it f} (kHz)');
ylabel('dB');
title('{\it N} = 4, Chebyshev - 1');
type = 2;
G0 = 0; G = 12; GB = 0.01; Gb = 9;
Dw = hpeqbw(N, G0, G, GB, Gb, Dwb, type);
[w1,w2] = bandedge(w0,Dw); f1 = w1*fs/2/pi; f2 = w2*fs/2/pi;
[B,A] = hpeq(N, G0, G, GB, w0, Dw, type);
H = 20*log10(abs(fresp(B,A,w)));
figure;
plot(f,H,'b-');
hold on;
ylim([-8 14]); ytick(-6:3:12);
xlim([0,20]); xtick(0:2:20);
grid;
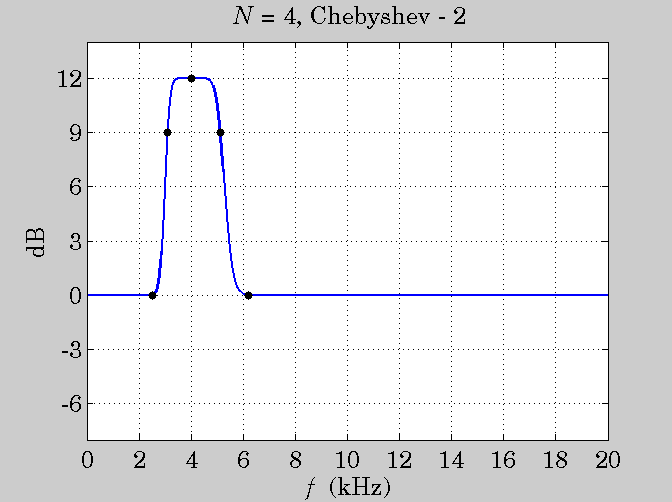
plot([fb1,f1,f0,f2,fb2], [Gb,GB,G,GB,Gb], 'k.', 'markersize',18);
hold off;
xlabel('{\it f} (kHz)');
ylabel('dB');
title('{\it N} = 4, Chebyshev - 2');
type = 3;
G0 = 0; G = 12; GB = 11.99; Gs = 0.01; Gb = 9;
Dw = hpeqbw(N, G0, G, GB, Gb, Dwb, type, Gs);
[w1,w2] = bandedge(w0,Dw); f1 = w1*fs/2/pi; f2 = w2*fs/2/pi;
[B,A] = hpeq(N, G0, G, GB, w0, Dw, type, Gs);
e = ripple(G,GB,G0); es = ripple(G,Gs,G0);
k1 = e/es; k = ellipdeg(N,k1);
Ws = tan(Dw/2)/k; Dws = 2*atan(Ws);
[w1s,w2s] = bandedge(w0,Dws); f1s = fs * w1s/2/pi; f2s = fs * w2s/2/pi;
H = 20*log10(abs(fresp(B,A,w)));
figure;
plot(f,H,'b-');
hold on;
ylim([-8 14]); ytick(-6:3:12);
xlim([0,20]); xtick(0:2:20);
grid;
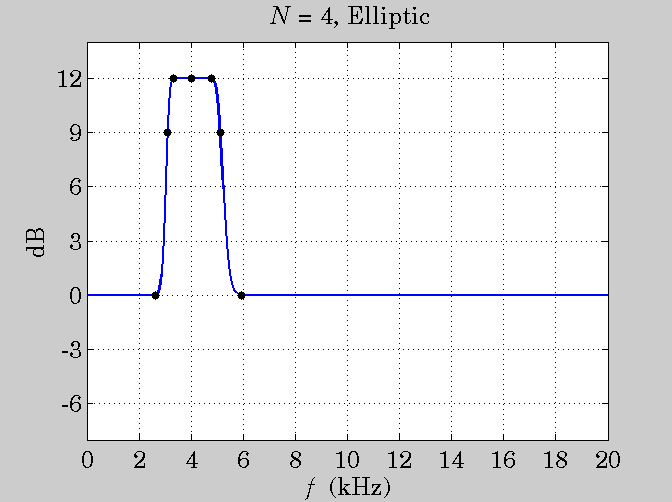
plot([f1s,fb1,f1,f0,f2,fb2,f2s], [Gs,Gb,GB,G,GB,Gb,Gs], 'k.', 'markersize',18);
hold off;
xlabel('{\it f} (kHz)');
ylabel('dB');
title('{\it N} = 4, Elliptic');