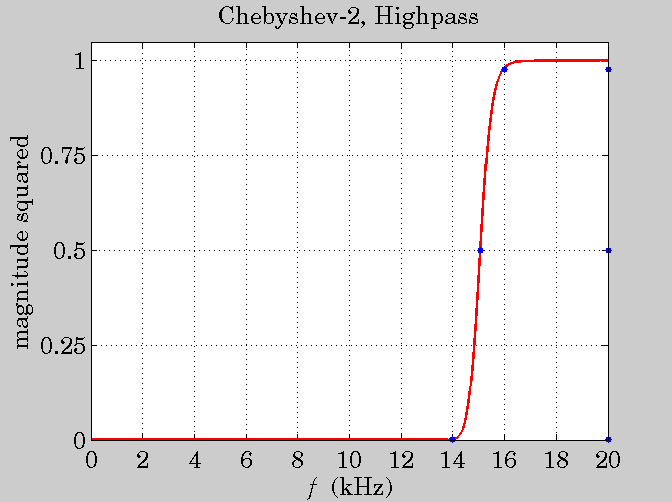
% ----------------------------------------------------------------------------
% Example output from hpeq.m
%
% Chebyshev type-2 highpass
% ----------------------------------------------------------------------------
% Sophocles J. Orfanidis
% ECE Department, Rutgers University
% 94 Brett Road, Piscataway, NJ 08854-8058
%
% Email:   orfanidi@ece.rutgers.edu
% Date:    June 15, 2005
%
% Reference: Sophocles J. Orfanidis, "High-Order Digital Parametric Equalizer
%            Design," J. Audio Eng. Soc., vol.53, pp. 1026-1046, November 2005.
%
% Web Page: http://www.ece.rutgers.edu/~orfanidi/hpeq
%
% tested with MATLAB R11.1 and R14
% ----------------------------------------------------------------------------

clear all;

fs=40; f1=14; f1s=16;
G0 = -Inf; G = 0; GB = -30; type = 2; Gs = -0.1;

w0=pi; Dw=2*pi*(20-f1)/fs; Dws=2*pi*(20-f1s)/fs;

Nexact = hpeqord(G0, G, GB, Gs, Dw, Dws, type),
N=ceil(Nexact)

[B,A,Bh,Ah] = hpeq(N, G0, G, GB, w0, Dw, type)

f = linspace(0,20,1001); w = 2*pi*f/fs;

H = abs(fresp(B,A,w)).^2;

Gb = -3; Dwb = bandwidth(N,G0,G,GB,Gb,Dw,type);                            % 3-dB width
[w1b,w2b] = bandedge(w0,Dwb); f1b = fs * w1b/2/pi; f2b = fs * w2b/2/pi;    % 3-dB frequencies

figure;
plot(f,H,'r-', [f1,f1b,f1s,20,20,20], 10.^([GB,Gb,Gs,GB,Gb,Gs]/10), 'b.');
ylim([0,1.05]); ytick(0:0.25:1);
xlim([0,20]); xtick(0:2:20);
title('Chebyshev-2, Highpass');
xlabel('{\it f}  (kHz)'); ylabel('magnitude squared')
grid;

Nexact =

    5.9021


N =

     6


B =

    1.0000         0         0         0         0
    0.6121    0.6912    0.6121         0         0
    0.4091    0.2589    0.4091         0         0
    0.2015   -0.2377    0.2015         0         0


A =

    1.0000         0         0         0         0
    1.0000    1.2647    0.7976         0         0
    1.0000    0.8607    0.4199         0         0
    1.0000    0.4517    0.0923         0         0


Bh =

    1.0000         0         0
    0.6121   -0.6912    0.6121
    0.4091   -0.2589    0.4091
    0.2015    0.2377    0.2015


Ah =

    1.0000         0         0
    1.0000   -1.2647    0.7976
    1.0000   -0.8607    0.4199
    1.0000   -0.4517    0.0923

Published with MATLAB® 7.0.4