% ----------------------------------------------------------------------------
% Example output from hpeq.m
%
% Chebyshev type-1 & type-2, boost
% ----------------------------------------------------------------------------
% Sophocles J. Orfanidis
% ECE Department, Rutgers University
% 94 Brett Road, Piscataway, NJ 08854-8058
%
% Email:   orfanidi@ece.rutgers.edu
% Date:    June 15, 2005
%
% Reference: Sophocles J. Orfanidis, "High-Order Digital Parametric Equalizer
%            Design," J. Audio Eng. Soc., vol.53, pp. 1026-1046, November 2005.
%
% Web Page: http://www.ece.rutgers.edu/~orfanidi/hpeq
%
% tested with MATLAB R11.1 and R14
% ----------------------------------------------------------------------------

clear all;

disp('% ---------- Chebyshev type-1 --------------------------------------------------');

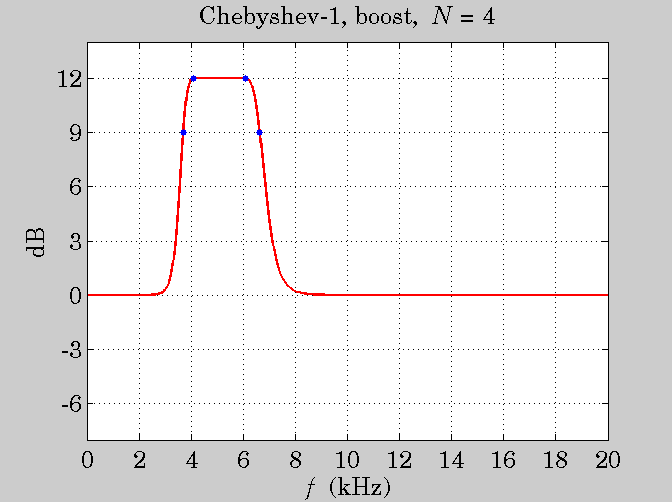
N = 4; fs = 40; f0 = 5; Df = 2; w0 = 2*pi*f0/fs; Dw = 2*pi*Df/fs;
G0 = 0; G = 12; GB = 11.99; type = 1;

[B,A,Bh,Ah] = hpeq(N, G0, G, GB, w0, Dw, type)

f = linspace(0,20,1001); w = 2*pi*f/fs;

H = 20*log10(abs(fresp(B,A,w)));

% H = 20*log10(abs(fresp(Bh,Ah,w,w0)));  % alternative computation of frequency response

[w1,w2] = bandedge(w0,Dw); f1 = fs * w1/2/pi; f2 = fs * w2/2/pi;

Gb = G-3; Dwb = bandwidth(N,G0,G,GB,Gb,Dw,type);                           % 3-dB width
[w1b,w2b] = bandedge(w0,Dwb); f1b = fs * w1b/2/pi; f2b = fs * w2b/2/pi;    % 3-dB frequencies

figure;
plot(f,H,'r-', [f1,f2,f1b,f2b],[GB,GB,Gb,Gb],'b.');
ylim([-8 14]); ytick(-6:3:12);
xlim([0,20]); xtick(0:2:20);
title('Chebyshev-1, boost, {\it N} = 4');
xlabel('{\it f}  (kHz)'); ylabel('dB');
grid;

disp('% ---------- Chebyshev type-2 --------------------------------------------------');

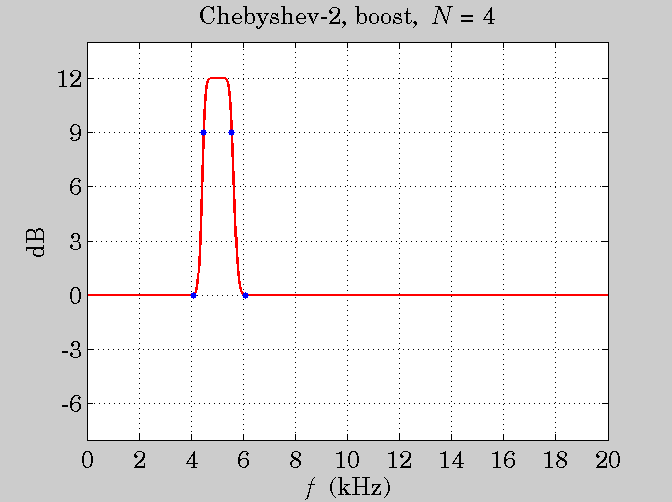
N = 4; fs = 40; f0 = 5; Df = 2; w0 = 2*pi*f0/fs; Dw = 2*pi*Df/fs;
G0 = 0; G = 12; GB = 0.01; type = 2;

[B,A,Bh,Ah] = hpeq(N, G0, G, GB, w0, Dw, type)

f = linspace(0,20,1001); w = 2*pi*f/fs;

H = 20*log10(abs(fresp(B,A,w)));

% H = 20*log10(abs(fresp(Bh,Ah,w,w0)));  % alternative computation of frequency response

[w1,w2] = bandedge(w0,Dw); f1 = fs * w1/2/pi; f2 = fs * w2/2/pi;

Gb = G-3; Dwb = bandwidth(N,G0,G,GB,Gb,Dw,type);                           % 3-dB width
[w1b,w2b] = bandedge(w0,Dwb); f1b = fs * w1b/2/pi; f2b = fs * w2b/2/pi;    % 3-dB frequencies

figure;
plot(f,H,'r-', [f1,f2,f1b,f2b],[GB,GB,Gb,Gb],'b.');
ylim([-8 14]); ytick(-6:3:12);
xlim([0,20]); xtick(0:2:20);
title('Chebyshev-2, boost, {\it N} = 4');
xlabel('{\it f}  (kHz)'); ylabel('dB');
grid;

% ---------- Chebyshev type-1 --------------------------------------------------

B =

    1.0000         0         0         0         0
    1.0926   -2.6387    3.2437   -2.1618    0.7554
    1.1550   -2.6119    2.8733   -1.6013    0.4404


A =

    1.0000         0         0         0         0
    1.0000   -2.5547    3.3101   -2.2458    0.7816
    1.0000   -2.4338    2.9315   -1.7793    0.5372


Bh =

    1.0000         0         0
    1.0926   -1.5465    0.7554
    1.1550   -1.3837    0.4404


Ah =

    1.0000         0         0
    1.0000   -1.6129    0.7816
    1.0000   -1.4420    0.5372

% ---------- Chebyshev type-2 --------------------------------------------------

B =

    1.0000         0         0         0         0
    1.1314   -3.0660    4.1730   -2.8731    0.9950
    0.9620   -2.4158    3.0151   -1.8905    0.5905


A =

    1.0000         0         0         0         0
    1.0000   -2.7349    3.7489   -2.5856    0.8944
    1.0000   -2.6039    3.3801   -2.1975    0.7126


Bh =

    1.0000         0         0
    1.1314   -2.0732    0.9950
    0.9620   -1.4925    0.5905


Ah =

    1.0000         0         0
    1.0000   -1.8678    0.8944
    1.0000   -1.6825    0.7126

Published with MATLAB® 7.0.4